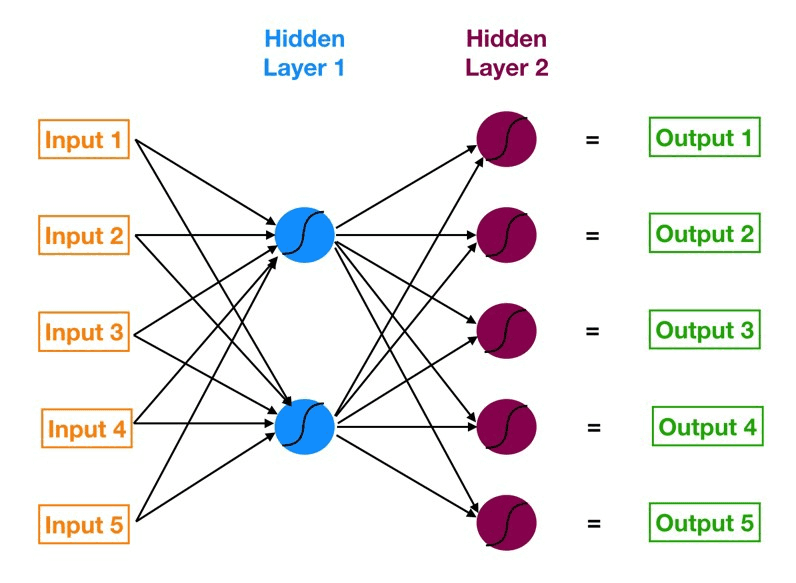
激活函数¶
实质是选择输出形式，一般情况下
- 连续值转为$(0,1)$概率输出选 sigmoid
- $(0,1)$ 概率输出且和为 1，选 softmax
- $(-1,1)$ 输出选 tanh
- 单边抑制选 ReLUs
Sigmoid¶
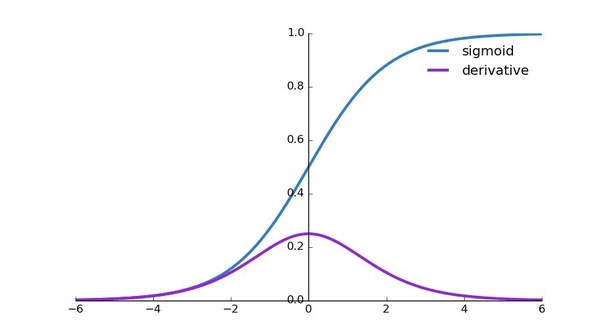$$
Sigmoid(x)=\sigma(x)=\frac{1}{1+e^{-x}}
$$
也可以表征信号强度。用于控制门时，1 表示完全打开，0 表示关闭 $$ \begin{aligned} \frac{\mathrm{d\sigma(x)}}{\mathrm{d} x} &=\frac{\mathrm{d}}{\mathrm{d} x}\left(\frac{1}{1+e^{-x}}\right) \\&=\frac{\mathrm{e}^{-x}}{\left(1+\mathrm{e}^{-x}\right)^{2}} \\&=\frac{e^{-x}}{1+e^{-x}} \frac{1}{1+e^{-x}} \\&=(1-\frac{1}{1+e^{-x}} )\frac{1}{1+e^{-x}} \\ &=\sigma(1-\sigma) \end{aligned} $$
ReLU¶
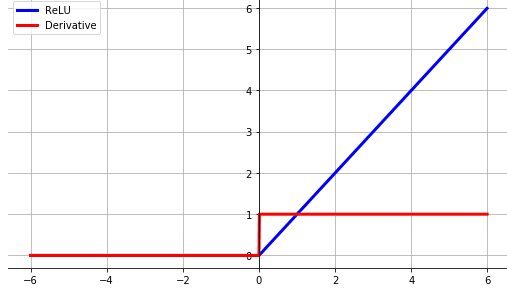$$
ReLU(x)=\max(0,x)
$$
单边抑制性源自生物学。
$$
\frac{\mathrm{d}}{\mathrm{d} x} \operatorname{ReLU}=\left\{\begin{array}{ll}{1} & {x \geqslant 0} \\ {0} & {x<0}\end{array}\right.
$$
LeakyReLU¶
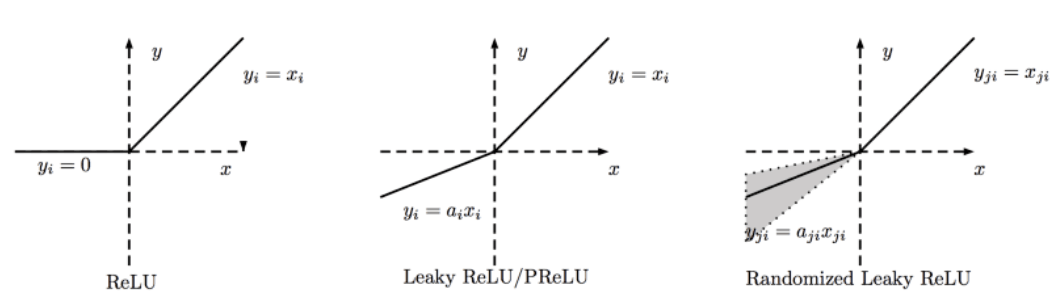
弥补 ReLU 在 $x<0$ 时会导致梯度消融的缺陷 $$ \text { LeakyReLU } =\left\{\begin{array}{ll}{x} & {x \geqslant 0} \\ {p x} & {x<0}\end{array}\right. $$ $p$ 是自行设置的较小超参数，比如 0.01 等。 $$ \frac{\mathrm{d}}{\mathrm{d} x} \text { LeakyReLU }=\left\{\begin{array}{ll}{1} & {x \geqslant 0} \\ {p} & {x<0}\end{array}\right. $$
tanh¶
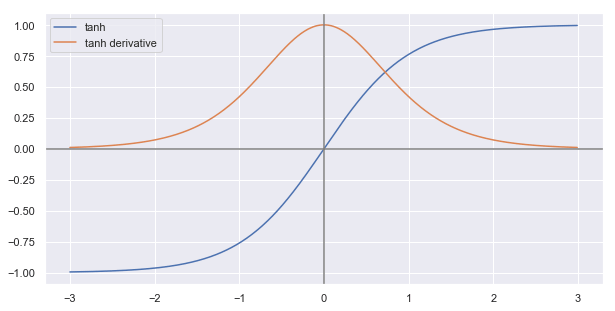$$
\tanh (x)=\frac{\left(e^{x}-e^{-x}\right)}{\left(e^{x}+e^{-x}\right)} =2 \cdot \operatorname{sigmoid}(2 x)-1
$$
控制输出和状态。可以视为 sigmoid 函数变换得到
$$
\begin{aligned} \frac{\mathrm{d}}{\mathrm{d} x} \tanh (x)=& \frac{\left(e^{x}+e^{-x}\right)\left(e^{x}+e^{-x}\right)-\left(e^{x}-e^{-x}\right)\left(e^{x}-e^{-x}\right)}{\left(e^{x}+e^{-x}\right)^{2}} \\ &=1-\frac{\left(e^{x}-e^{-x}\right)^{2}}{\left(e^{x}+e^{-x}\right)^{2}}=1-\tanh ^{2}(x) \end{aligned}
$$
SoftMax¶
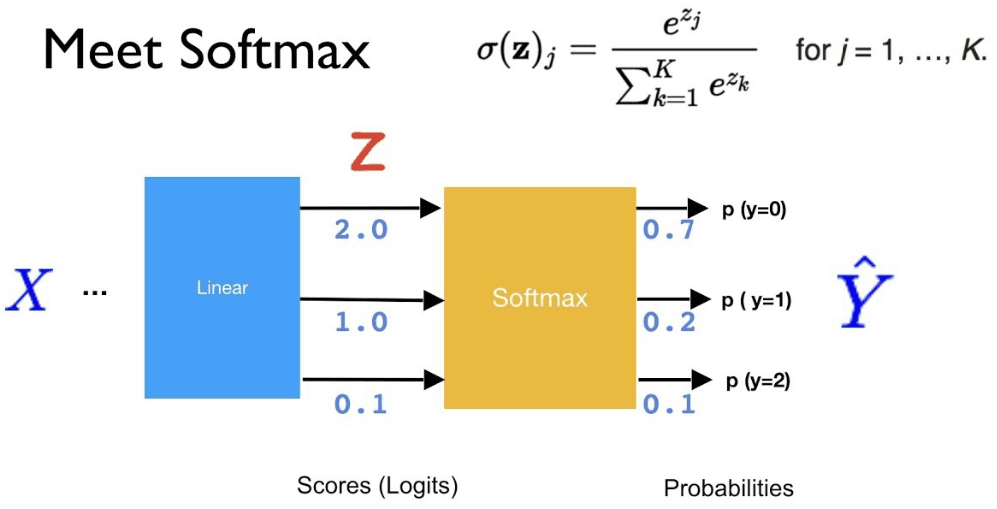
求梯度 $$ \frac{\delta S_{i}}{\delta x_{j}}=\frac{\delta \frac{e^{x_{i}}}{\sum_{k=1}^{N} e^{x_{k}}}}{\delta x_{j}} $$ 对$f(x) = \frac{g(x)}{h(x)}$，有$f^{\prime}(x)=\frac{g^{\prime}(x) h(x)-h^{\prime}(x) g(x)}{[h(x)]^{2}}$，这里 $g_{i} =e^{x_{i}}, h_{i} =\sum_{k=1}^{N} e^{x_{k}}$ $$ \frac{\delta g_{i}}{\delta x_{j}}=\left\{\begin{array}{ll}{e^{x_{j}},} & {\text { if } i=j} \\ {0,} & {\text { otherwise }}\end{array}\right.\\ \frac{\delta h_{i}}{\delta x_{j}}=\frac{\delta\left(e^{x_{1}}+e^{x_{2}}+\ldots+e^{x_{N}}\right)}{\delta x_{j}}=e^{x_{j}} $$
- $i=j$
- $i \neq j$
矩阵形式 $$ \frac{\delta S}{\delta x}=\left[\begin{array}{ccc}{\frac{\delta S_{1}}{\delta x_{1}}} & {\cdots} & {\frac{\delta S_{1}}{\delta x_{N}}} \\ {\ldots} & {\frac{\delta S_{i}}{\delta x_{j}}} & {\cdots} \\ {\frac{\delta S_{N}}{\delta x_{1}}} & {\cdots} & {\frac{\delta S_{N}}{\delta x_{N}}}\end{array}\right]\\ \frac{\delta S}{\delta x}=\left[\begin{array}{ccc}{\sigma\left(x_{1}\right)-\sigma\left(x_{1}\right) \sigma\left(x_{1}\right)} & {\dots} & {0-\sigma\left(x_{1}\right) \sigma\left(x_{N}\right)} \\ {\cdots} & {\sigma\left(x_{j}\right)-\sigma\left(x_{j}\right) \sigma\left(x_{i}\right)} & {\cdots} \\ {0-\sigma\left(x_{N}\right) \sigma\left(x_{1}\right)} & {\cdots} & {\sigma\left(x_{N}\right)-\sigma\left(x_{N}\right) \sigma\left(x_{N}\right)}\end{array}\right]\\ \frac{\delta S}{\delta x}=\left[\begin{array}{ccc}{\sigma\left(x_{1}\right)} & {\dots} & {0} \\ {\dots} & {\sigma\left(x_{j}\right)} & {\dots} \\ {0} & {\dots} & {\sigma\left(x_{N}\right)}\end{array}\right]-\left[\begin{array}{ccc}{\sigma\left(x_{1}\right) \sigma\left(x_{1}\right)} & {\dots} & {\sigma\left(x_{1}\right) \sigma\left(x_{N}\right)} \\ {\cdots} & {\sigma\left(x_{j}\right) \sigma\left(x_{i}\right)} & {\cdots} \\ {\sigma\left(x_{N}\right) \sigma\left(x_{1}\right)} & {\dots} & {\sigma\left(x_{N}\right) \sigma\left(x_{N}\right)}\end{array}\right] $$
反向传播¶
$w^l_{jk}$ 表示$(l-1)$层第 $j$ 个输入到 $l$ 层第 $k$ 个输出的权重
$b^l_{j}$ 表示$l$层偏置
$z^l_{j}$ 表示 $l$ 层第 $j$ 个神经元的输入：$z_{j}^{l}=\sum_{k} w_{j k}^{l} a_{k}^{l-1}+b_{j}^{l}$
$a^l_j$ 表示 $l$ 层第 $j$ 个神经元的输出：$a_{j}^{l}=\sigma\left(\sum_{k} w_{j k}^{l} a_{k}^{l-1}+b_{j}^{l}\right)$
$\sigma$ 表示激活函数
$C$ 表示损失函数
$L$ 为神经网络最大层数
$l$ 层第 $l$ 个神经元的误差为 $\delta_{j}^{l}=\frac{\partial C}{\partial z_{j}^{l}}$
- 最后一层
$\odot$ 表示 Hadamard 乘积，对应项元素相乘
- 中间任意两层间的损失
- 权重梯度
- 偏置梯度
损失函数¶
均方误差（MSE）¶
$$ \mathcal{L}=\frac{1}{2} \sum_{k=1}^{K}\left(y_{k}-o_{k}\right)^{2} $$$o_k$ 为预测输出值，$\frac{1}{2}$作为常数方便求解梯度 $$ \begin{aligned} \frac{\partial \mathcal{L}}{\partial o_{i}}&=\frac{1}{2} \sum_{k=1}^{K} \frac{\partial}{\partial o_{i}}\left(y_{k}-o_{k}\right)^{2}\\ &=\frac{1}{2} \sum_{k=1}^{K} 2 \cdot\left(y_{k}-o_{k}\right) \cdot \frac{\partial\left(y_{k}-o_{k}\right)}{\partial o_{i}}\\ &=\sum_{k=1}^{K}\left(y_{k}-o_{k}\right) \cdot(-1) \cdot \frac{\partial o_{k}}{\partial o_{i}} \\ &=\sum_{k=1}^{K}\left(o_{k}-y_{k}\right) \cdot \frac{\partial o_{k}}{\partial o_{i}} \end{aligned} $$ 当且仅当 $k = i$ 时 $\frac{\partial o_{k}}{\partial o_{i}}=1$，即结点误差只与结点本身相关。 $$ \frac{\partial \mathcal{L}}{\partial o_{i}}=o_i-y_i $$
交叉熵损失¶
$$ H(p \| q)=-\sum_{i} p(i) \log _{2} q(i) = H(p)+D_{K L}(p \| q)\\ D_{K L}(p \| q)=\sum_{i} p(i) \log \left(\frac{p(i)}{q(i)}\right) $$对分类问题，经 one-hot 编码，$H(p)=0$，进而有 $$ H(p \| q)=D_{K L}(p \| q) =\sum_{j} y_{j} \log \left(\frac{y_{j}}{o_{j}}\right) =1 \cdot \log \frac{1}{o_{i}}+\sum_{j \neq i} 0 \cdot \log \left(\frac{0}{o_{j}}\right) =-\log o_{i} $$ 由极大似然估计可得对数交叉熵损失为 $$ \mathcal{L}=-\sum_{k} y_{k} \log \left(p_{k}\right) $$ 考虑对自变量 $z_i$ 求偏导 $$ \frac{\partial \mathcal{L}}{\partial z_{i}}=-\sum_{k} y_{k} \frac{\partial \log \left(p_{k}\right)}{\partial z_{i}}=-\sum_{k} y_{k} \frac{\partial \log \left(p_{k}\right)}{\partial p_{k}} \cdot \frac{\partial p_{k}}{\partial z_{i}}=-\sum_{k} y_{k} \frac{1}{p_{k}} \cdot \frac{\partial p_{k}}{\partial z_{i}} $$ 输出分布 $p$ 为 SoftMax 时，将求和展开成两类情况的和 $$ \frac{\partial \mathcal{L}}{\partial z_{i}}=-y_{i}\left(1-p_{i}\right)-\sum_{k \neq i} y_{k} \frac{1}{p_{k}}\left(-p_{k} \cdot p_{i}\right)=p_{i}\left(y_{i}+\sum_{k \neq i} y_{k}\right)-y_{i} $$ 对分类情况而言 $\sum_{k} y_{k}=1,y_{i}+\sum_{k \neq i} y_{k}=1$，此时 $$ \frac{\partial \mathcal{L}}{\partial z_{i}}=p_i-y_i $$
学习优化¶
挑战¶
病态。特别是海森矩阵。随机梯度下降会‘‘卡’’ 在某些情况，此时即使很小的更新步长也会增加代价函数。
局部极小值。数量众多，代价不定
- 高原、鞍点与平坦区域
- 梯度爆炸和梯度消融
- 悬崖
基本算法¶
Nesterov 动量中，梯度计算在施加当前速度之后。因此，Nesterov 动量可以解释为往标准动量方法中添加了一个校正因子。
自适应学习率¶
经验上，从训练开始时积累梯度平方会导致有效学习率过早和过量的减小。
修改 AdaGrad 以在非凸情景下效果更好，改变梯度积累为指数加权的移动平均。
批正则化¶
应用于全连接/卷积层之后，非线性层（激活）之前。加速学习，降低初始依赖。 $$ x_{i} \longleftarrow \gamma \frac{x_{i}-\mu_{B}}{\sqrt{\sigma_{B}^{2}+\epsilon}}+\beta $$ $\epsilon$ 是很小的常数防止除零。$\gamma,\beta$ 是超参数保证变换后的 $x_i$ 能具有任意标准差与均值，此时的均值只与 $\beta$ 有关，之前的均值还和其他时步关联，变换后更容易用 SGD 学习。
算法实现¶
- 导入相关库
import math
import copy
import numpy as np
- 硬件与版本信息
%load_ext watermark
%watermark -m -v -p ipywidgets,numpy
- 辅助函数设计
def batch_iterator(X, y=None, batch_size=64):
n_samples = X.shape[0]
for i in np.arrange(0, n_samples, batch_size):
begin, end = i, min(i+batch_size, n_samples)
if y is not None:
yield X[begin:end], y[begin:end]
else:
yield X[begin:end]
- 损失函数
class CrossEntropy(object):
def __init__(self):
pass
def loss(self, y, pred):
p = np.clip(p, 1e-15, 1-1e15)
return -y * np.log(p) - (1-y) * np.log(1-p)
def acc(self, y, pred):
return np.sum(y==pred, axis=0) / len(y)
def gradient(self, y, pred):
p = np.clip(p, 1e-15, 1-1e15)
return - (y / p) + (1 - y) / (1-p)
- 优化器
class RMSProp(object):
def __init__(self, learning_rate=0.01, rho=0.9):
self.learning_rate = learning_rate
self.Eg = None
self.eps = 1e-8
self.rho = rho
def update(self, w, grad_w):
if self.Eg is None:
self.Eg = np.zeros(np.shape(grad_w))
self.Eg = self.rho * self.Eg + (1 - self.rho) * np.power(grad_w, 2)
return w - self.learning_rate * grad_w / np.sqrt(self.Eg + self.eps)
- Dense 层实现
class Dense(object):
'''全连接层
parameters:
---------------
n_units: int
该层神经元数量
input_shape: tuple
该层期望接收的输入规格
'''
def __init__(self, n_units, input_shape=None):
self.layer_input = None
self.input_shape = input_shape
self.n_units = n_units
self.trainable = True
self.W = None
self.b = None
def set_input_shape(self, shape):
self.input_shape = shape
def initialize(self, optimizer):
limit = 1 / math.sqrt(self.input_shape[0])
self.W =np.random.uniform(-limit, limit, (self.input_shape[0], self.n_units))
self.b = np.zeros((1,self.n_units))
self.W_opt = copy.copy(optimizer)
self.b_opt = copy.copy(optimizer)
def layer_name(self):
return self.__class__.__name__
def parameters(self):
return np.prod(self.W.shape) + np.prod(self.b.shape)
def forward(self, X, training=True):
self.layer_input = X
return X.dot(self.W) + self.b # 无激活函数
def backward(self, accum_grad):
W = self.W
if self.trainable:
grad_w = self.layer_input.T.dot(accum_grad)
grad_b = np.sum(accum_grad, axis=0, keepdims=True)
self.W = self.W_opt.update(self.W, grad_w)
self.b = self.b_opt.update(self.b, grad_b)
accum_grad = accum_grad.T.dot(W.T)
return accum_grad
def output_shape(self):
return (self.n_units,)
- 神经网络
class NeuralNetwork(object):
'''全连接神经网络
parameters：
----------------
optimizer: class
最小化损失时的优化器
loss：class
度量性能的损失函数。这里是交叉熵损失
validation: tuple
验证集（X,y）
'''
def __init__(self, optimizer, loss, validation_data=None):
self.optimizer = optimizer
self.layers = []
self.errors = {'training':[],'validation':[]}
self.loss = loss()
self.val_set = None
if validation_data is not None:
X, y = validation_data
self.val_set = {'X':X, 'y':y}
def set_trainable(self, trainable):
'''设置是否更新层中参数'''
for layer in self.layers:
layer.trainable = trainable
def add(self, layer):
if self.layers:
layer.set_input_shape(shape = self.layers[-1].output_shape())
if hasattr(layer, 'initialize'):
layer.initialize(optimizer = self.optimizer)
self.layers.append(layer)
def test_on_batch(self, X, y):
y_pred = self._forward(X, training=False)
loss = np.mean(self.loss.loss(y, y_pred))
acc = self.loss.acc(y, y_pred)
return loss, acc
def train_on_batch(self, X, y):
y_pred = self._forward(X)
loss = np.mean(self.loss.loss(y, y_pred))
acc = self.loss.acc(y, y_pred)
loss_grad = self.loss.gradient(y, y_pred)
self._backward(loss_grad=loss_grad)
return loss, acc
def fit(self, X_train, y_train, n_epochs, batch_size):
for _ in range(n_epochs):
batch_error = []
for X_batch, y_batch in batch_iterator(X_train, y_train, batch_size):
loss, _ = self.train_on_batch(X_batch, y_batch)
batch_error.append(loss)
self.errors['training'].append(np.mean(batch_error))
if self.val_set is not None:
val_loss, _ = self.test_on_batch(self.val_set['X'], self.val_set['y'])
self.errors['validation'].append(val_loss)
return self.errors['training'], self.errors['validation']
def _forward(self, X, training=True):
layer_output = X
for layer in self.layers:
layer_output = layer.forward(layer_output, training)
return layer_output
def _backward(self, loss_grad):
for layer in self.layers:
loss_grad = layer.backward(loss_grad)
def predict(self, X_test):
return self._forward(X_test, training=False)